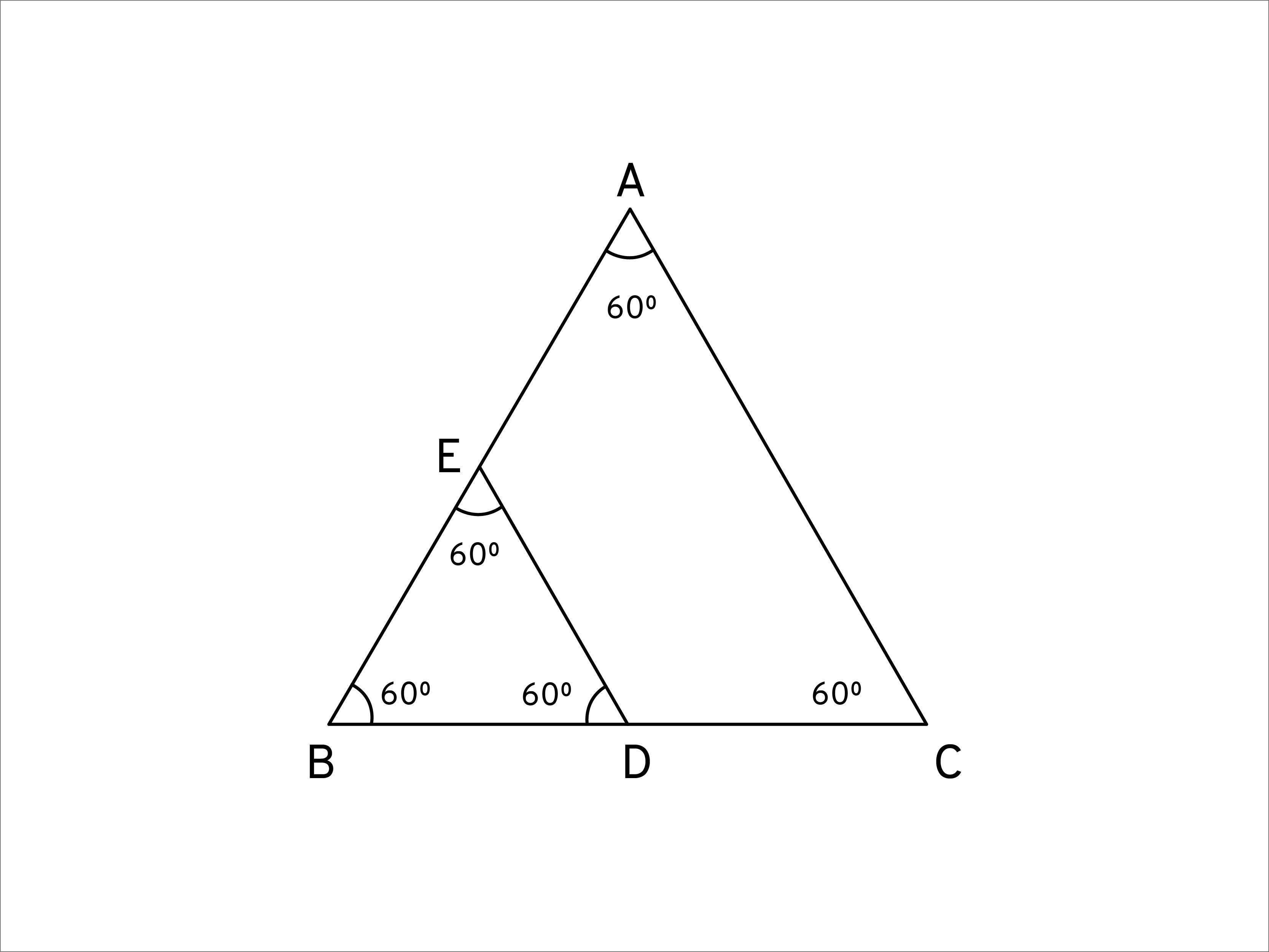
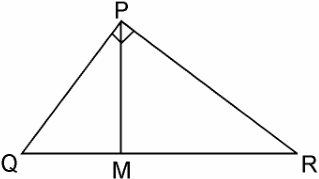
Ncert solutions mathematics class 10 Solutions for Chapter 6 triangles
Exercises in Chapter 6 triangles Grade 10
Questions in Triangles – Exercise 6.1
Questions in Triangles – Exercise 6.2
Questions in Triangles – Exercise 6.3
Questions in Triangles – Exercise 6.4
Questions in Triangles – Exercise 6.5
Questions in Triangles – Exercise 6.6
Was This helpful?
Chapters in this book